Why it's ridiculously dumb having a 100% random password

Topic: Why it's ridiculously dumb having a 100% random password (Read 8052 times) previous topic - next topic

0 Members and 2 Guests are viewing this topic.

Re: Why it's ridiculously dumb having a 100% random password

Reply #90 – 05 February 2023, 01:07:32

You're missing the point still.
If you are so sure of your theory go and discuss it with folk who are capable of debunking it fully. And possibly even interested?
Places where you'll find experts in the subject with 'some real maths balls of steel'.
Create your haveged issue and demolish the project. Enjoy

I'm going out on a limb here but I don't think anyone here is interested? Or if they are they're not really engaging with you.

Re: Why it's ridiculously dumb having a 100% random password

Reply #91 – 05 February 2023, 02:08:53

In my option the best thing to do going forward is to put your theories into code.
Once it is coded then the users of your application will be able use the better security offered if you are correct in your line of reasoning.

While I did find a few posts mathematically interesting, it is not something I want to dive into.
I think the chances of this esoteric subject of another Artix user to get into mathematic proofs would be extremely low.
An university, encryption or similar technology forum would be better suited for these detailed math discussions.

PS: I find the personal jabs/jokes/attacks sprinkled through this thread to be in poor taste.

Re: Why it's ridiculously dumb having a 100% random password

Reply #92 – 05 February 2023, 03:12:33

I did try to look up some of the concepts here, and found some suggestions that the best password scheme is to use random passwords but minus "obvious" ones like those appearing in hacked password lists and dictionaries and so on. The concept of "pure randomness" does seem to be acknowledged as lacking, if you fail to filter out the "abc123" "my-pa55w0rd" and similar results that are possible to randomly procure. But does this relate to hashed strings, which is the way almost all passwords are stored? Have you found evidence that they are somehow more predictable or obvious if they do not fit your criteria?

Code: [Select]

$ echo "123" |sha256sum
181210f8f9c779c26da1d9b2075bde0127302ee0e3fca38c9a83f5b1dd8e5d3b  -
$ echo "124" |sha256sum
ca2ebdf97d7469496b1f4b78958f9dc8447efdcb623953fee7b6996b762f6fff  -
$ echo "38r@ywf%o6u?" |sha256sum
d6f717645c7f437e8b38a426c782105d0c43f5e8762037ebd1718065a9a1ba5c  -
$ echo "111" |sha256sum
1fc917c7ad66487470e466c0ad40ddd45b9f7730a4b43e1b2542627f0596bbdc  -
$ echo "222" |sha256sum
8f8eea956d0ea50d6442fdab213326f75bb6f584268b0795ad452faa85db5f9d  -

Regardless of the strength of the initial password, it apparently results in the same length hash that is equally unclear as to it's origins unless you try and guess the initial one and compare the hash. If you have indeed found some weakness in the hash values from certain passwords, then that must be a flaw in the hashing algorithm which would be especially interesting.

Re: Why it's ridiculously dumb having a 100% random password

Reply #93 – 06 February 2023, 08:56:38

Quote from: Surf3r – on 05 February 2023, 00:20:46

No matter if Gripped gets gripped again or lq doesn't have an iq or me being the Big Foot, Yeti or a green little martian with a peanut brain, things are the way I've presented no matter if we like it or not and can be debunked only thru MATHEMATICAL means not thru swears jokes, curses, voodoo, referendum, coin flips, raffles or sending anybody on Mars or other even more exotic planets or places.

Any jokes etc etc will count as a loss. If anyone has some real math balls of steel please step forward and start debunking (good luck with that too)

lol,

entropy or chaos is not static, as you keep repeating, but dynamic and that's why your imaginary hacker can't guess anything.
Because you asshole don't want to understand that, the discussion is over for me.

Re: Why it's ridiculously dumb having a 100% random password

Reply #94 – 10 February 2023, 07:42:29

Quote from: ####### – on 05 February 2023, 03:12:33

Have you found evidence that they are somehow more predictable or obvious if they do not fit your criteria?

If a string is vulnerable (weak) its hash is vulnerable (weak). Nobody would bother reverse engineer the hash algorithm itself since it can search for unfortunate random easy cakes that produces easy hashes. And all hashing algorithms have collisions that basically means instead of 1 solution (hash) there are 2 or 3 depending on the algorithm. So when adding to the party the hash algo instead of complicating the problem it makes it easier as a hacker doesn't care it really broke your unique hash or its doppelganger derived from a different string and not yours.

And speaking of random again maybe you guys can throw a look into this ASLR
and this reducing entropy

"In many systems, 2^N can be in the thousands or millions; on modern 64-bit systems, these numbers typically reach the millions at least, Hector Marco-Gisbert and Ismael Ripoll showed in 2014 how to bypass the ASLR in 64-bit systems in less than one second under certain circumstances.[5] For 32-bit systems at 2004 computer speeds which have 16 bits for address randomization, Shacham and co-workers state "... 16 bits of address randomization can be defeated by a brute force attack within minutes"

This was back in 2014, 9 years later I guess they found even better ways of sneaking thru our random 'safe heavens'

Re: Why it's ridiculously dumb having a 100% random password

Reply #95 – 10 February 2023, 19:13:42

True randomness has always been a concern since the first computer was created.
Nothing can beat the randomness of swirling cooling hot liquid.

I think that most of the stuff encrypted can be broken with the right tools and powerful enough system.
It all boils down to just a matter of time to get it cracked.

The best one can do is try to minimize the foot print for attack by using different user names and accounts that are not linked together in any fashion so if one breaks one is not completely exposed.

Personally all the breaches in my information security have been the result of the major companies and government databases being cracked and not from my passwords being hacked.

Re: Why it's ridiculously dumb having a 100% random password

Reply #96 – 30 March 2023, 18:13:40

So here's the latest development on the realm of patterns in case anyone missed new things I've 'cracked'.

Because it looks like things do not scale the way I've deduced. Was a deduction not a demonstration even if it made a lot of sense

So things get more nuanced. And the place they nuance the most is where the string length S = T (T is total pwd ingredients used)

Pattern variant calculations seem to scale as follow, deduced from crash testing strings. When I say crash testing I mean generating
their brute arrangements and verify how it matches deductions, and there are mixed results.

So starting from 3x3, 4x4, 5x5, 6x6, 7x7 and have to see If my machine can resist a 8x8 or a 9x9 string crash test
would be awesome 😄

The results are as follow

3x3 (abc) best pattern is 21 match deduced formula A[T,(S-1)]*3(S-2)
4x4 (abcd)    211    match deduced formula A[T,(S-1)]*3(S-2)
5x5 (abcde)    2111 doesn't match but still best pattern deduced thru crash test

Now here starts the funny part

6x6 (abcdef) best pattern is claimed by 2211   no longer 21111 as previously thought
7x7 (abcdefg) 22111 no longer   211111
8x8 (abcdefgh) not yet crash tested but it may preserve   221111 and no longer 2111111

Now when 9x9 (abcdefghi) there's a big chance were going to see a 222111 for the best bbp

If this squeeze of a 2 inside best patterns every 3 (T x S) when T=S (key aspect! T=S) remains constant we can deduce or even
demonstrate a formula but now there's a question how we can be sure when 'reach' these out of touch strings like 94x94 (T=S=94)
if we wouldn't see some best patterns like 44433322211111 etc

When T is significantly bigger than S there are slim chances for a better patterns than that wit ONE rep char. i.e. 2111111

I'll try next to crash test a 8x8 and a 9x9 to see if best patterns gonna kick another 2 in or not or even a 3 who knows

If we can somehow obtain a mathematically working formula for these mixed arrangements thru which we can determine accurately
the exact way these patterns and their corresponding variant number scale we would be real scientists. 😛

Re: Why it's ridiculously dumb having a 100% random password

Reply #97 – 04 April 2023, 00:53:18

Got news again. I'll be short and eventually will update. Here's the catch. Those ONE rep. strings have a weakness in fact, all have but we just need to crack their secrets. So the thing is as follow and checked + double checked. For the first factor I've nailed it from the start it's A[T,(S-1) but second is not as straight forward cos belongs to a so called recurrence relation not a 1st degree equation, more accurately these kinda sequences are called triangle sequence. So here is the way a ONE repetition string scale its variant numbers, , the general formula:

   A[T, (S-1)] * [S*(S-1)]/2   S≥3

So let's say we have a 7 long string and ONE repeats like i.e.   aabcdef   will match 211110 bbp,
let's say we have 10 total elements T=10, S=7

A(10,6) * [S*(S-1)]/2) = (10!/4!) * [7*(7-1)]/2 = 3.175.200

while NO rep

A(10,7) = 604.800    meaning about 5.25 smaller

Other bbp have different sequence of course but they tend to have a higher amplification factor but there isn't that much to amplify like in the ONE rep. strings. When tend to reach symmetry like for a 10x10 string where T=S=10 the bigger bbp will have not ONE but more char that repeat, have to determine their sequence

Factorials tend to land on these recurrent relations.

I'll try to reverse engineer a 221110   to find their sequence, at first hand they seem to like bigger amplification factor like 15/45/105

Instead of a 3 it start straight up with a 15 but loses big time from its first factor

EDIT: done it deduced properly the sequence for a 221..like bbp

A[T,(S-2)] * S!/8((S-4)    S ≥ 5 cos 2+2+1 has to be at least 5

As a conclusion I've greatly underestimated the amplification factor these multiple twos like bbp ca give at the right S length not just always

As a change the ONE rep 211..like bbp becomes more powerful than a NO rep 111.. bbp much earlier that previously though at S=14
not at 25. It looks like once string length S is increased closer to T we tend to have an even amount of TWOS and ONES.

Still the previous conclusion of undesirable RANDOM generator holds the line as NOTHING can guarantee generating a weak string.

Repetitions are good in certain amount but NOT with a GRC level repetition .

So there's a moment when you have to have a 2, another longer string to have double 2, triple 2 and so on

EDIT2 : In the meantime bellow are couple of formulas specific for each bbp. I'll add more once I 'crack' them.

T,S ∈ ℕ ,   T ≥ 1 , S ≥ T

A(T,S) 1...........1 NO repetition string S ≥ 1

A[T,(S-1)]*S!/2(S-2)!    21.........0 ONE rep. S ≥ 3

A[T,(S-2)]*S!/8(S-4)! 221......00    TWO reps. S ≥ 5

A[T,(S-3)]*S!/48(S-6)!    2221...000 THREE reps. S ≥ 7

Edit3: Added the so called universal formula that gives the shear number of variants for any T of any S for any amount of twos from 1 to infinity. This is the most numerous/predominant/relevant bbp. Other bbp with threes, fours or fives at very best can equal if at all those with twos but never exceed them. See print screen bellow the GOLDEN formula

Re: Why it's ridiculously dumb having a 100% random password

Reply #98 – 08 April 2023, 17:14:50

Now after the decisive help from Artix devs and community primarily @nous and @replabrobin I've managed to have a script derived from the above universal formula found by myself

And I'm gonna use an example and put the script bellow. So to use this script you have to feed it 3 values. Two of which generally will be the same and the 3rd will be used to sample different values to determine what the string needs to have. So if we have a T=94, an S=63 and an n=3 (meaning testing the result when we have 3 reps like this, 2221111111....)

We will feed the perl script script like this:

Code: [Select]

./count.pl 94 63 3

the e+122 means 10^ in this case 10^122

We will try multiple values of n till we get the highest possible value vs that when n=3

After we reach some maximum value if we still increase n, the value will start falling meaning we already found the best value of n for that particular T and S see print screen

When T=94, S=63, n=3 we will have ~ 3.75×10^116 222111111111111 ...till reach 63
When T=94, S=63, n=14 => 1.22×10^122 (best possible) 222222222222221 ...till reach 63

Total possible is 94^63=2×10^124

A string that belongs to the 2nd pattern in this examples has ~ 325.294 more variants than the 1st, yes 325 thousand times stronger than the 1st

And here's the perl script, currently doesn't accept n=0 but you can improve it if you want or wait till I figure it out

Of course first make the script executable

Code: [Select]

#!/usr/bin/perl
use strict;
no strict 'refs';
use warnings;
use 5.36.0;

die "Usage: $0 <T: total elements> <S: pass length> <n: number of twos>" if $#ARGV < 2;

our ($T, $S, $n) = (int $ARGV[0], int $ARGV[1], int $ARGV[2]);

for (qw/T S n/) {
    die "$$_ not a positive integer" if !($$_ > 0);
}
die "Not T>S" if ($S > $T);
die "Not n<S" if ($n > $S);
die "Not S-n<T" if ($S-$n > $T);
die "Not 2n<S" if (2*$n > $S);

my $Z=$S-$n;
my $k=2*$n;
#        T! /    (T-Z)! *     S! / [(2^n) *   n!   *  (S-k)! ]
say fact($T)/fact($T-$Z)*fact($S)/((2**$n)*fact($n)*fact($S-$k));

sub fact {
    return 0 if (my $f = shift) == 0;
    my ($i, $p) = (1, 1);
    $p *= $_ foreach ($i++ .. $f);
    return $p;
}

Re: Why it's ridiculously dumb having a 100% random password

Reply #99 – 21 April 2023, 16:49:13

Rather big step forward in this project. Managed to deduce a formula that gives the result no matter what we have twos/threes/fours etc. However did not deduced yet a mix between them like 3322211 or 43111 etc . But for now any mix like 2211 or 33111 or 44411 555551111 271111 etc bellow formula can accurately give the exact result. For this another factorial parameter m stepped in (m!)

m it's the value that shows up in the bbp i.e. for 22222211111 our m =2! for 444441111111 etc our m=4!

The goal is to deduce a formula that covers every possible mix of patterns not only between m and ones.

The challenge is that for something like 54321...its S=15 is huge. To deduce that there' need to crash test a 15x15 which implies a supercomputer unless this can be deduce thru a mathematical demonstration.

I'll make a python script that asks for m along T, S and n but here's the formula.

EDIT: While working on the python script the Z (zipped string length) can be calculated as follow

Z = S-n(m-1)

this is because Z parameter value changes as a function of S, n and m

Edit2: Here's the python script. If it throws an error (negative...) it's because for that S, you choose either an m or an n that exceed the S value. S can not be smaller than m or n amount etc. Final result gives 2 formats (integers, the most accurate and decimal format) for the ease of result evaluation

Code: [Select]

# Online Python - IDE, Editor, Compiler, Interpreter
T = int(input("T: "))
S = int(input("S: "))
m = int(input("m: "))
n = int(input("n: "))
Z = int(S)-int(n)*(int(m)-int(1))    # S-n(m-1)
k = int(m)*int(n)
import math
a = math.factorial(T)
b = math.factorial(T-Z)
c = math.factorial(S)
d = math.factorial(n)*math.factorial(m)**n*math.factorial(S-k)
e = int(a)*int(c)
f = int(b)*int(d)
g = (e/f)
print(g)
print(int(g))

Re: Why it's ridiculously dumb having a 100% random password

Reply #100 – 24 April 2023, 17:44:20

Well, guess what guys, I've done it. Found the Universal formula for Mixed Arrangements. This formula can accurately calculate the exact amount of possibilities a certain bbp has, no matter how many elements repeat or not or in which way. This eventually can be used to evaluate the quality of any string random generated or not. The quality of a string is higher when its backbone has a bigger amount of variants that can be built on the back of that same particular pattern. But let's dive into the deepest possible rabbit hole of the arrangements.

The 'm' is the repeating element. If an element repeats 5 times m5=5

Depending on the mix of repeating elements we will have different 'ems' i.e. m5=5, m3=3, m2=2 when we have a bbp like 53211111...
(note we can not have an m=1 as that it's not a repeating element, m can be either 0 meaning no repeating element or from 2 and up)
m symbolizes we have reps in our string bbp

Depending on how many 'ems' we have into the string were gonna have their corresponding ''ens' i.e. m5 has an n5, an m3 has an n3 an m2 has an n2 etc
(note that n can be 1 as that indicates that an m5=5 shows up only once so n5=1 if m5 shows up 5 times m5 will have a corresponding n5=5

Gonna take a bigger example:

Let's take this bbp 66 5 44 3 2222 111111
We will have m6=6 and n6=2, m5=5 and n5=1, m4=4 and its n4=2, m3=3 and n3=1, m2=2 and its n2=4 (no m1 to be considered)
When we have no 'ems' we can consider m=0 and n=0, basically the formula will fallback on simple arrangements
Z - is zipped string length from above example Z=16 (bbp has 16 digits)
S - unzipped string, or the length of the pwd here S=6+6+5+4+4+3+2+2+2+2+1+1+1+1+1+1=42
T - total elements considered to choose from i.e. T=94 (a-Z, 0-9, symbols ; 26+26+10+32=94, without space symbol)
S ≤ T
K=m*n
The last factor (S-k2-k3..)! can be calculated much simple as follow. Subtract from string length S=42 any repeats 42-6-6-5-4-4-3-2-2-2-2=42-36=6 (we do not subtract from S any 1 but repeats only) Now let's try calculate how many strings this bbp has 66 5 44 3 2222 111111 T=94 S=42 Z=16

A(94,16)*42!/(6!)^2*2!*(5!)^1*(4!)^2*2!*(3!)^1*(2!)^4*4! = 9,6×10³⁰ × 5,9×10³³ = etc..

I'll get done a python script that will do all these nasty calc automatically

Re: Why it's ridiculously dumb having a 100% random password

Reply #101 – 25 May 2023, 08:57:09

Some news.

Submitted my mixed arrangements formula on OEIS. The editors there approved it but later on they said was approved by mistake..

Idk how the hell you can approve by mistake such things..Now it has the proposal status.

The formula is checked and ultra checked at this stage there's no error in it.

EDIT: it was approved by 'mistake' twice. Also what I've learned there's no really reject. Is approved or not. Those sequences that are erroneous or don't met certain requirements receive the keyword dumb or are deleted completely which isn't the case. In this case editors did not agree with the Mixed Arrangements title./name given by me. I did not agree to change the name though.

Re: Why it's ridiculously dumb having a 100% random password

Reply #102 – 13 June 2023, 11:19:16

Now manged to put together a python script that calculates:

1 Total number of variants. (in two formats, decimal and integer for better/quicker evaluation).
2 Prints Z, the number of unique elements for that pattern.(zipped string length)
3 Prints the number of possible variants derived from that pattern. (gives two formats, decimal and integer for quick view)
4 Prints the percentage from the total variants (the bigger the better)

When T<S still patterns are ways to sum to S but from T number of factors. e.g. T=3 S=8 patterns can have 3 factors at the most
e.g. 5 2 1 but not 4 2 1 1 cos that belongs to a T=4 not 3.

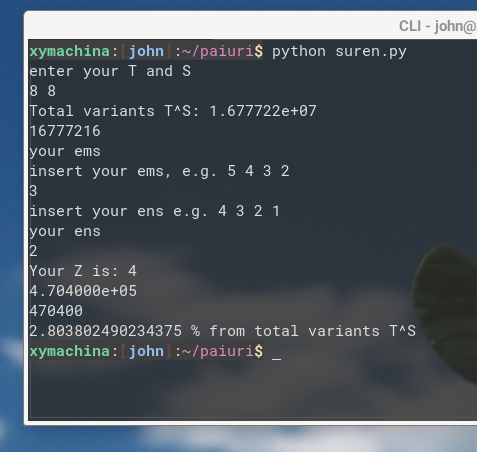
Now to give an example for T=8, S =8, pattern 33110000 see print screen. When there's no repeating elements in the pattern
just hit enter for ems and for ems (m will be considered 0 meaning no rep. elements in the pattern)

And here's the fixed script with the help of @suren

EDIT: Added python-mpmath syntax (needs mpmath module to be installed) and changed, 'int' with 'abs' for higher accuracy

Code: [Select]

print("enter your T and S")
T, S = map(int, input().split())

#T=94
#S=16

J = T**S 
print('Total variants T^S:', (format(J, "e")))
print(J)

print("your ems")
print("insert your ems, e.g. 5 4 3 2")
array1 = list(map(int, input().split()))

print("insert your ens e.g. 4 3 2 1")
print("your ens")
array2 = list(map(int, input().split()))

# Resize the arrays by filling with zeros
array1 = array1 + [0, 0, 0, 0]
array2 = array2 + [0, 0, 0, 0]

m7, m6, m5, m4 = array1[:4]
n7, n6, n5, n4 = array2[:4]

ens = int(n7) + int(n6) + int(n5) + int(n4)
kmn = int(m7) * int(n7) + int(m6) * int(n6) + int(m5) * int(n5) + int(m4) * int(n4)
Z = int(ens) + (S - kmn)
#print(kmn)
print('Your Z is:', int(Z))

import mpmath

# Set the desired precision
mpmath.mp.dps = 1000

a = mpmath.factorial(T)
b = mpmath.factorial(T-Z)
#print(b)
c = mpmath.factorial(S)
p = mpmath.factorial(n7)*(mpmath.factorial(m7))**n7
o = mpmath.factorial(n6)*(mpmath.factorial(m6))**n6
j = mpmath.factorial(n5)*(mpmath.factorial(m5))**n5
w = mpmath.factorial(n4)*(mpmath.factorial(m4))**n4
dum = p*o*j*w*mpmath.factorial(S-kmn)
#print(dum)
e = abs(a)/abs(b)
f = abs(c)/abs(dum)
#print(f)
g = abs(e)*abs(f)
#print(format(g, "e"))
print(int(g))
#print(f"{e:,}")
h = g/J
l = h * 100
#print(l, '%')
#print(l,"% from total variants T^S")

EDIT:

Discussion about this topic moved here on github